FRACTIONS
I. Simplifying Fractions: To simplify a fraction remove factors of 1.
This is done by factoring completely both numerator and denominator, then remove any unnecessary 1's. For example:
II. Multiplying fractions
A. Follow the steps in I for each of the fractions to be multiplied together.
B. Be sure to reduce any factor appearing in both the numerator and denominator of any fraction.
C. Be very careful to transfer all remaining factors to your answer from your problem. (This is a very common error.)
III. Dividing fractions
A. Always invert the divisor or divisors first, then proceed with the multiplication steps.
B. Follow all the steps in II.
IV. Finding the lowest common denominator (LCD)
A. Make sure each denominator is a factor of the LCD, and make sure the LCD is the smallest number possible.
B. Always factor completely each denominator before trying to find the LCD.
C. A good sure way of not getting too many or too few terms in your LCD is:
1. Write the prime factors of each denominator and place like factors under like factors.
2. Take one common factor from each column.
3. If you have not made any errors, this should combine to be your lowest common denominator.
4. Example: Find the LCD of 8, 16, 12, 20
8 = 2 2 2 16 = 2 2 2 2 12 = 2 2 3 20 = 2 2 5 LCD = 2 2 2 2 3 5 or 24 3 5 Example: Find the LCD of 2x-10x+12x, 2x4-8x2, and x-x-6
2x-10x+12x = 2 x (x - 2) (x - 3) 2x4-8x2 = 2 x x (x - 2) (x + 2) x - x - 6 = (x + 2) LCD = 2 x x (x - 2) (x - 3) (x + 2)
V. Combining algebraic fractions
A. Find the LCD by IV.
B. Change them to equivalent fractions (fractions with like denominators).
C. Combine numerators and reduce to lowest terms over the LCD.
VI. Changing signs of fractions
A. We have three signs to consider: That of the numerator, denominator and fraction.
B. Rules:
1. Change every sign in both numerator and denominator.
2. Change every sign in the numerator only provided you change the sign of the fraction.
3. Change every sign in the denominator only provided you change the sign of the fraction.
C. This can be helpful in finding similar lowest common denominators.
VII. Mixed expressions
A. To change a mixed expression to a fraction, consider the whole number as a fraction with the denominator of one.
B. Then proceed as in addition or subtraction of fractions. (combining fractions)
BE CAREFUL OF YOUR NEGATIVE SIGNS
VIII. Compound fractions
A. Numerator and/or denominator is in the form of a fraction.
B. General form:
C. Procedure:
1. Simplify
as far as possible. It may involve addition or subtraction of fractions.
2. Simplify
as far as possible, as in step C1.
D.
means
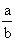
Therefore, proceed as in part III.
IX. Fractions in equations
A. Find the LCD.
B. Multiply each term in the equation by the LCD. This includes everything on both sides of the equation. Factor wherever possible.
WHAT YOU DO TO ONE SIDE OF THE EQUATION, YOU MUST DO TO THE OTHER SIDE, THAT MEANS THE WHOLE SIDE.
C. This will give a new equation, all the denominators being gone. Complete the solution.
D. Make sure that no solution makes a denominator in the original equation equal to zero. If it does through it out.
FRACTION.HDT