Review questions: Logarithms TRUE or FALSE MATH 121

I. The exponential function b^x = y

______ a.          domain (x) is all Real Numbers

______ b.          domain may include Z⁺, Z^-, Q ⁺, Q ^-, I⁺, I^-

______ c.          b is always > 0

______ d.          Range (b^x) is always > 0

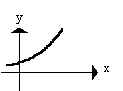
______ e.          If b > 1, graph looks like:   

______ f.          If b < 1, graph looks like: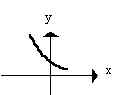       

______ g.          If b < 0, graph looks like :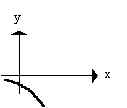        

II. The logarithmic function Log_bx = y

______ a.          is the inverse of y = b^x

______ b.          domain (x) > 0

______ c.          Range (y) is all reals

______ d.          If graph of y = b^x is                 

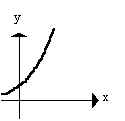
                         then graph of log_bx = y is            

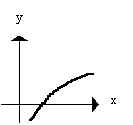
______ e.          b is always positive (usually > 1)

______ f.         b ≠ 1

______ g.          y = log_bx is equivalent to b^y = x

III.

______ a.          A log can be negative.

______ b.          You can take the log of a negative number.

______ c.          A log can be 0.

______ d.          You can take the log of 0.

______ e.          log_bx - 1 = log_b(x - 1)

page 2

______ f.          log_b(x - 1) = log_bx - log_b1

______ g.          log_bx^(1/2) = 1/2 log_bx =

______ h.           = log_bx - log_b2

______ i.         

______ j.          (log_bx)³ = 3 log_bx

______ k.          (x - 1)log 3 = x log 3 - log 3

______ l.          = 2

______ m.          log_bbⁿ = n

______ n.          = N

______ o.          log_b1 = 0

______ p.          If 0 < N < 1, then log N < 0

______ q.          log_b(xb) = log_bx + 1

______ r.          If f is an exponential function and f(2) = , then f(x) = 3^-x

______ s.          If f is an exponential function and f(2) = , then b = -3

______ t.           If log_(1/3)x = -2, then log₃ = -2