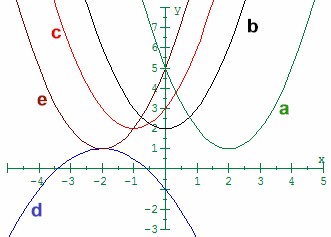
- y − 2 = (x + 1)2 ________
- y − 1 = -½(x + 2)2 ________
- y − x2 = 2 ________

- y = x2 + 4x + 5 ________

- y = x2 − 4x + 5 ________

|
 |
| 16. -3 (a double root) ____________ | 17. 5, -3 ____________ |
| 18. 2 + √5, 2 − √5 ____________ | 19. 4, ¾ ____________ |
| 20. 3i, -3i ____________ | 21. 5 + 3i, 5 − 3i ____________ |
|
1. c 2. d 3. b 4. e 5. a 9. (-4, 5) 10. all reals |
|
|